机器学习笔记7 高偏差/低偏差，学习曲线，模型选择

Andrew Ng cs229 Machine Learning 笔记

原文：https://share.coursera.org/wiki/index.php/ML:Advice_for_Applying_Machine_Learning

面对一个机器学习问题，我们提取好特征，挑选好训练集，选择一种机器学习算法，然后学习预测得到了第一步结果。然而我们不幸地发现，在测试集上的准确率低得离谱，误差高得吓人，要提高准确率、减少误差的话，下一步该做些什么呢？

可以采用以下的方法来减少预测的误差：

  • 获得更多的训练样本
  • 减少特征的数量
  • 增加特征的数量
  • 使用多项式特征
  • 增大或减小正则化参数$\lambda$

但不要盲目在这些可行的方法里随便选一种来提升模型，需要用一些诊断模型的技术来帮助我们选择使用哪种策略。

1.评估假设

即使模型假设对于训练集的误差很低，若存在过拟合，模型的预测也同样会不准确。

给定一份训练集，我们可以将数据分成两部分：训练集和测试集。

  1. 使用训练集最小化$J(\Theta)$得到$\Theta$参数
  2. 计算测试集的误差：
$$J_{test}(\Theta) = \dfrac{1}{2m_{test}} \sum_{i=1}^{m_{test}}(h_\Theta(x^{(i)}_{test}) - y^{(i)}_{test})^2$$

3.计算分类错误率（即0/1分类错误率）

$$err(h_\Theta(x),y) = \begin{matrix} 1 & \mbox{if } h_\Theta(x) \geq 0.5\ and\ y = 0\ or\ h_\Theta(x) < 0.5\ and\ y = 1\newline 0 & \mbox otherwise \end{matrix}$$

测试集的平均误差为：

$$\large \text{Test Error} = \dfrac{1}{m_{test}} \sum^{m_{test}}_{i=1} err(h_\Theta(x^{(i)}_{test}), y^{(i)}_{test})$$

也就是测试集上分类错误的样本的比例。

2.模型选择与训练/验证/测试集

  • 学习算法若仅仅对训练集拟合较好，并不能说明其假设也是好的。
  • 训练集上的假设误差通常要比其他数据集上得到的误差要小。

为了在假设上选择模型，可以测试模型的多项式的次数来观察误差结果。

无验证集

  1. 对不同的多项式次数的模型通过训练集得到最优化参数$\Theta$。
  2. 找到在预测集上误差最小的模型的多项式次数$d$。
  3. 使用测试集估计泛化误差$J_{test}(\Theta^{(d)})$。

在这个例子中，我们用测试集训练得到的一个变量，即多项式次数$d$，但这样做会使其他数据集的误差更大。

为了解决这个问题，我们引入了第三种数据集，即交叉验证集(Cross Validation Set)，来作为选择$d$的中间数据集。这样，测试集会给出一个准确，非乐观估计的误差结果。

例如，将数据集分成三份：

  • 训练集：60%
  • 交叉验证集：20%
  • 测试集：20%

对于这三个数据集我们可以计算三个不同误差值：

有验证集

  1. 对不同的多项式次数的模型通过训练集得到最优化参数$\Theta$。
  2. 找到在验证集上误差最小的模型的多项式次数$d$。
  3. 使用测试集估计泛化误差$J_{test}(\Theta^{(d)})$。

使用验证集则避免了使用测试集来确定多项式次数$d$。

3.诊断偏差 vs. 方差

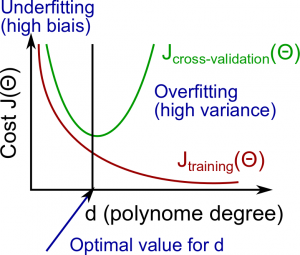
我们来讨论一下多项式次数$d$和过拟合以及欠拟合之间的关系。

  • 我们需要区分导致预测结果差的原因是偏差还是方差。
  • 高偏差也就是欠拟合，高方差也就是过拟合。我们需要在这两者之间找到一个黄金分割。

随着多项式次数$d$的增加，训练集的误差会减少。

同时，交叉验证集的误差会随着$d$的增加而减少，但在$d$增加到某一点之后，会随着$d$的增加而增加，形成一个凸曲线

  • 高偏差（欠拟合）：$J_{train}(\Theta)$和$J_{CV}(\Theta)$都较高，并且$J_{CV}(\Theta) \approx J_{train}(\Theta)$。
  • 高方差（过拟合）：$J_{train}(\Theta)$较低，且$J_{CV}(\Theta)$比$J_{train}(\Theta)$高得多。

可以用下图来表示：

Features-and-polynom-degree

4.正则化和偏差/方差

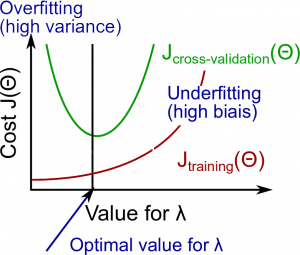
下面来分析正则化参数$\lambda$。

  • $\lambda$较大：高偏差（欠拟合）
  • $\lambda$不大不小：正好
  • $\lambda$较小：高方差（过拟合）

较大的$\lambda$参数会惩罚$\Theta$参数，即简单化结果函数的曲线，造成欠拟合。

$\lambda$和训练集以及验证集的关系如下：

  • $\lambda$较小：$J_{train}(\Theta)$较低，且$J_{CV}(\Theta)$较高（高方差/过拟合）。
  • $\lambda$不大不小：$J_{train}(\Theta)$和$J_{CV}(\Theta)$都较低，并且$J_{CV}(\Theta) \approx J_{train}(\Theta)$。
  • $\lambda$较大：$J_{train}(\Theta)$和$J_{CV}(\Theta)$都较高（高偏差/欠拟合）。

下图说明了$\lambda$值和假设之间的关系：

Features-and-lambda

为了选择模型和正则化参数$lambda$，我们需要：

  1. 列出$\lambda$测试的值，比如 $\lambda \in \lbrace0, 0.01, 0.02, 0.04, 0.08, 0.16, 0.32, 0.64, 1.28, 2.56, 5.12, 10.24\rbrace$；
  2. 选择一个$\lambda$的值进行计算；
  3. 创建模型集，比如按照多项式次数或其他指标来创建；
  4. 选择一个模型来学习$\Theta$值；
  5. 用所选的模型学习得到$\Theta$值，使用选择的$\lambda$值计算$J_{train}(\Theta)$（为下一步学习参数$\Theta$）；
  6. 使用学习（带$\lambda$）得到的参数$\Theta$计算不带正则项或是$\lambda=0$的训练误差$J_{train}(\Theta)$；
  7. 使用学习（带$\lambda$）得到的参数$\Theta$计算不带正则项或是$\lambda=0$的交叉验证误差$J_{CV}(\Theta)$；
  8. 对模型集合所有$\lambda$取值重复上述步骤，选择使交叉验证集误差最小的组合；
  9. 如果需要使用图形化结果来帮助决策的话，可以绘制$\lambda$和$J_{train}(\Theta)$的图像，以及$\lambda$和$J_{CV}(\Theta)$的图像；
  10. 使用最好的$\Theta$和$\lambda$组合，在测试集上进行预测计算$J_{test}(\Theta)$的值来验证模型对问题是否有好的泛化能力。
  11. 为了帮助选择最好的多项式次数和$\lambda$的值，可以采用学习曲线来诊断。

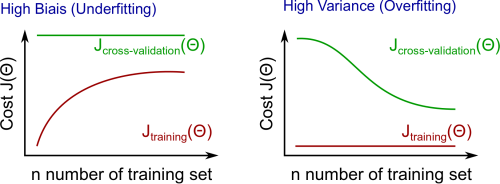
5.学习曲线

训练3个样本很容易得到0误差，因为我们永远可以找到一条二次曲线完全经过3个点。

  • 当训练集越来越大时，二次函数的误差也会增加。
  • 误差值会在训练集大小m增加到一定程度后慢慢平缓。

高偏差的情况

  • 小训练集：$J_{train}(\Theta)$较低，$J_{CV}(\Theta)较高。
  • 大训练集：$J_{train}(\Theta)$和$J_{CV}(\Theta)都较高，并且$J_{train}(\Theta) \approx J_{CV}(\Theta)$。

如果学习算法有高偏差的问题，那么获取更多的训练数据并不会有很多改进。

对于高方差的问题，对于训练集大小有如下关系：

高方差的情况

  • 小训练集：$J_{train}(\Theta)$较低，$J_{CV}(\Theta)较高。
  • 大训练集：$J_{train}(\Theta)$会略微增加，$J_{CV}(\Theta)会略微降低，并且$J_{train}(\Theta) < J_{CV}(\Theta)$。

如果学习算法有高方差的问题，那么获取更多的训练数据是有用的。

下图展示了训练集大小和高偏差/高方差问题之间的关系。

High-variance-high-bias

6.再次考虑如何选择提升模型的下一步

决策过程可以分解成以下几点：

  • 获得更多的训练样本
    • 解决高方差
  • 减少特征的数量
    • 解决高方差
  • 增加特征的数量
    • 解决高偏差
  • 使用多项式特征
    • 解决高偏差
  • 增加正则参数$\lambda$
    • 解决高偏差
  • 减少正则参数$\lambda$
    • 解决高方差

7.诊断神经网络

  • 参数较少的神经网络很容易欠拟合，但同时计算也较容易。
  • 参数较多的大型神经网络更容易过拟合，但同时计算量较大。在这种情况下可以使用正则化（增加$\lambda$）来避免过拟合问题。

使用单个隐藏层是一个较好地开始默认设置。你可以使用验证集在多个隐藏层上训练神经网络。

8.模型选择总结

以下是机器学习诊断的一些总结

  • 选择多项式次数M
  • 如何选择模型中得参数$\Theta$（即模型选择）

有3种方式解决：

  1. 获取更多数据（非常困难）
  2. 选择拟合数据最好且没有过拟合的模型（非常困难）
  3. 通过正则化来减少过拟合的机会

偏差：近似误差（预测值和期望值之间的差值）

  • 高偏差 = 欠拟合（BU）
  • $J_{train}(\Theta)$和$J_{CV}(\Theta)都较高，并且$J_{train}(\Theta) \approx J_{CV}(\Theta)$

方差：有限数据集之间的估计误差值

  • 高方差 = 过拟合（VO）
  • $J_{train}(\Theta)$较低，并且$J_{train}(\Theta) << J_{CV}(\Theta)$

偏差-方差权衡的直觉

  • 复杂模型=>数据敏感=>受训练集X变化的影响=>高方差，低偏差
  • 简单模型=>更死板=>不受训练集X变化的影响=>低方差，高偏差

机器学习的最重要的目标之一：找到一个模型在偏差-方差的权衡之间刚刚好。

正则化影响

  • $\lambda$值较小（过拟合）使模型容易受噪声影响，导致高方差。
  • $\lambda$值较大（欠拟合）会将参数值接近于0，导致高偏差。

模型复杂度影响

  • 多项式次数较低的模型（模型复杂度低）有高偏差和低方差。在这种情况下，模型拟合总是很差。
  • 多项式次数较高的模型（模型复杂度高）拟合训练集极好，拟合测试集极差。导致训练集上低偏差，但高方差。
  • 在现实中，我们想要选择一个模型在以上两种情况之间，既然可以很好地拟合数据，也有很好地泛化能力。

使用诊断时的一些典型经验法则

  • 获取更多地训练样本可以解决高方差问题，不能解决高偏差问题。
  • 减少特征数量可以解决高方差问题，不能解决高偏差问题。
  • 增加特征数量可以解决高偏差问题，不能解决高方差问题。
  • 增加多项式特征和交互特征（特征和特征交互）解决高偏差问题，不能解决高方差问题。
  • 当使用梯度下降时，减少正则化参数$\lambda$值可以解决高方差问题，增加$\lambda$值可以解决高偏差问题。
  • 当使用神经网络时，小型神经网络更容易欠拟合，大型神经网络更容易过拟合。交叉验证是选择神经网络大小的一种方式。

参考：