Andrew Ng cs229 Machine Learning 笔记
神经网络
非线性假设
在特征变量数较大的情况下,采用线性回归会很难处理,比如我的数据集有3个特征变量,想要在假设中引入所有特征变量的平方项:
$$g(\theta_0 + \theta_1x_1^2 + \theta_2x_1x_2 + \theta_3x_1x_3 + \theta_4x_2^2 + \theta_5x_2x_3 + \theta_6x_3^2 )$$
共有6个特征,假设我们想知道选取其中任意两个可重复的平方项有多少组合,采用允许重复的组合公式计算$\frac{(n+r-1)!}{r!(n-1)!}$,共有$\frac{(3 + 2 - 1)!}{(2!\cdot (3-1)!)} = 6$种特征变量的组合。对于100个特征变量,则共有$\frac{(100 + 2 - 1)!}{(2\cdot (100-1)!)} = 5050$个新的特征变量。
可以大致估计特征变量的平方项组合个数的增长速度为$\mathcal{O}(\frac{n^2}2)$,立方项的组合个数的增长为$\mathcal{O}(n^3)$。这些增长都十分陡峭,让实际问题变得很棘手。
在变量假设十分复杂的情况下,神经网络提供了另一种机器学习算法。
神经元和大脑
神经网络是对大脑工作方式的一种简单模拟。有证据表明,大脑对所有的功能(如视觉,触觉,听觉等)都采用了一种“学习算法”。将听觉皮层和视觉神经连接到一起,听觉皮层可以学会“看见”。这种理论叫作“neuroplasticity”,已经得到了很多例子和实验验证。
模型表达
简单来说,每个神经元都有输入(树突dendrites)和输出(轴突axons)。在模型中,输入就是我们的特征变量,输出就是模型假设的结果。
在神经网络中,分类问题通常采用logistic函数,也叫做sigmoid激活函数(sigmoid activation function)。$\theta$参数有时也被称为权重(weights)。
下面是一种简单的神经网络:
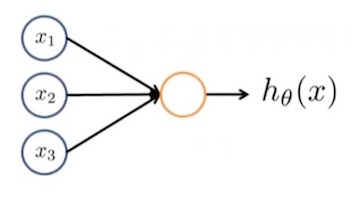
第一层是输入节点(nodes),第二层是输出节点,也就是我们假设函数的结果$h_{\theta}(x)$。
第一层叫作“输入层”(input layer),最后一层叫作“输出层”(output layer),输入层和输出层之间还可以有多层,统称为“隐藏层”(hidden layer)。如下图中,第二层就叫隐藏层。隐藏层节点表示为$a^2_0 \cdots a^2_n$,被称作“激活单元(activation units)”。
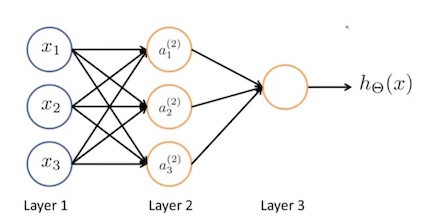
$a_i^{(j)}$表示第$j$层的$i$单元被“激活”,$\Theta^{(j)}$表示从第$j$层到第$j+1$层的权重矩阵。
上图的神经网络中,激活单元的计算分别为:
$$
\begin{align*}
a_1^{(2)} = g(\Theta_{10}^{(1)}x_0 + \Theta_{11}^{(1)}x_1 + \Theta_{12}^{(1)}x_2 + \Theta_{13}^{(1)}x_3) \newline
a_2^{(2)} = g(\Theta_{20}^{(1)}x_0 + \Theta_{21}^{(1)}x_1 + \Theta_{22}^{(1)}x_2 + \Theta_{23}^{(1)}x_3) \newline
a_3^{(2)} = g(\Theta_{30}^{(1)}x_0 + \Theta_{31}^{(1)}x_1 + \Theta_{32}^{(1)}x_2 + \Theta_{33}^{(1)}x_3) \newline
h_\Theta(x) = a_1^{(3)} = g(\Theta_{10}^{(2)}a_0^{(2)} + \Theta_{11}^{(2)}a_1^{(2)} + \Theta_{12}^{(2)}a_2^{(2)} + \Theta_{13}^{(2)}a_3^{(2)}) \newline
\end{align*}
$$
每一层都有自己的权重矩阵$\Theta^{(j)}$,如果第$j$层有 $s_j$ 个单元,第$j+1$层有$s_{j+1}$个单元,则$\Theta^{(j)}$是$s_{j+1} \times (s_j+1)$的矩阵。”+1”是因为第$j$层包括一个”偏差节点(bias nodes)“,$x_0$和$\Theta_0^{(j)}$。换句话说,输出节点不包括偏差节点,但输入节点会包括偏差节点。
举个例子,第一层有2个输入节点,第二层有4个激活单元。$\Theta^{(1)}$的维度为$4 \times 3$。
下面将以上模型表达向量化。
采用$z^{(i)}_k$表示$g$函数的输入,那么有:
$$
\begin{align*}
a_1^{(2)} = g(z_1^{(2)}) \newline
a_2^{(2)} = g(z_2^{(2)}) \newline
a_3^{(2)} = g(z_3^{(2)}) \newline
\end{align*}
$$
给定第$j$层的节点$k$,变量$z$等于:
$$
z_k^{(j)} = \Theta_{k,0}^{(j-1)}x_0 + \Theta_{k,1}^{(j-1)}x_1 + \cdots + \Theta_{k,n}^{(j-1)}x_n
$$
$x$和$z^{(j)}$的向量表示为:
$$
\begin{align*}
x =
\begin{bmatrix}
x_0 \newline
x_1 \newline
\cdots \newline
x_n
\end{bmatrix} &
z^{(j)} =
\begin{bmatrix}
z_1^{(j)} \newline
z_2^{(j)} \newline
\cdots \newline
z_n^{(j)}
\end{bmatrix}
\end{align*}
$$
因此,$z^{(j}) = \Theta^{(j-1)} x$
令$x = a^{(j-1)}$,则$z^{(j)} = \Theta^{(j-1)}a^{(j-1)}$
最后的结果为
$$
h_\Theta(x) = a^{(j+1)} = g(z^{(j+1)}) = g(\Theta^{(j)}a^{(j)})
$$
神经网络拟合逻辑运算
- $x_1\ AND\ x_2$
神经网络模型:
$$
\begin{align*}
\begin{bmatrix}
x_0 \newline
x_1 \newline
x_2
\end{bmatrix} \rightarrow
\begin{bmatrix}
g(z^{(2)})
\end{bmatrix} \rightarrow
h_\Theta(x)
\end{align*}
$$
其中,$x_0$为偏差,恒等于1。
权重参数为:
$\Theta^{(1)} =
\begin{bmatrix}
-30 & 20 & 20
\end{bmatrix}$
仅当$x_1$和$x_2$同时为1时,$h_{\Theta}(x) = 1$。
\begin{align*}
& h_\Theta(x) = g(-30 + 20x_1 + 20x_2) \newline
\newline
& x_1 = 0 \ \ and \ \ x_2 = 0 \ \ then \ \ g(-30) \approx 0 \newline
& x_1 = 0 \ \ and \ \ x_2 = 1 \ \ then \ \ g(-10) \approx 0 \newline
& x_1 = 1 \ \ and \ \ x_2 = 0 \ \ then \ \ g(-10) \approx 0 \newline
& x_1 = 1 \ \ and \ \ x_2 = 1 \ \ then \ \ g(10) \approx 1
\end{align*}
- $x_1\ NOR\ x_2$, $NOR$为$NOT\ OR$
模型同上,权重参数为:
$\Theta^{(1)} =
\begin{bmatrix}
10 & -20 & -20
\end{bmatrix}$
仅当$x_1$和$x_2$同时为0时,$h_{\Theta}(x) = 1$。
- $x_1\ OR\ x_2$
模型同上,权重参数为:
$\Theta^{(1)} =
\begin{bmatrix}
-10 & 20 & 20
\end{bmatrix}$
当$x_1$和$x_2$不同时为0时,$h_{\Theta}(x) = 1$。
- $x_1\ XNOR\ x_2$,$XNOR$为$NOT\ XOR$
将前面得到的模型组合起来$x_1\ XNOR\ x_2 = (x_1\ AND\ x_2)\ OR\ (x_1\ XOR\ x_2)$
模型如下:
$$
\begin{align*}
\begin{bmatrix}
x_0 \newline
x_1 \newline
x_2
\end{bmatrix} \rightarrow
\begin{bmatrix}
a_1^{(2)} \newline
a_2^{(2)}
\end{bmatrix} \rightarrow
\begin{bmatrix}
a^{(3)}
\end{bmatrix} \rightarrow
h_\Theta(x)
\end{align*}
$$
第一层到第二层的$\Theta^{(1)}$分别表示$AND$和$NOR$操作:
$$
\Theta^{(1)} =
\begin{bmatrix}
-30 & 20 & 20 \newline
10 & -20 & -20
\end{bmatrix}
$$
第二层到第三层的$\Theta^{(2)}$表示$OR$操作:
$$
\Theta^{(2)} =
\begin{bmatrix}-10 & 20 & 20\end{bmatrix}
$$
多类分类问题
输出用向量来表示多类分类问题:
$$
\begin{align*}
\begin{bmatrix}
x_0 \newline
x_1 \newline
x_2 \newline
\cdots \newline
x_n
\end{bmatrix} \rightarrow
\begin{bmatrix}
a_0^{(2)} \newline
a_1^{(2)} \newline
a_2^{(2)} \newline
\cdots
\end{bmatrix} \rightarrow
\begin{bmatrix}
a_0^{(3)} \newline
a_1^{(3)} \newline
a_2^{(3)} \newline
\cdots
\end{bmatrix} \rightarrow \cdots \rightarrow
\begin{bmatrix}
h_\Theta(x)_1 \newline
h_\Theta(x)_2 \newline
h_\Theta(x)_3 \newline
h_\Theta(x)_4 \newline
\end{bmatrix} \rightarrow
\end{align*}
$$
最后的结果:
$$h_\Theta(x) =
\begin{bmatrix}
0 \newline
0 \newline
1 \newline
0 \newline
\end{bmatrix}$$
表示该样本属于第三类,$h_{\Theta}(x)_3$。

