Andrew Ng cs229 Machine Learning 笔记

有监督学习

先理清几个概念：

$x^{(i)}$表示”输入”变量(“input” variables)，也称为特征值(features)。
$y^{(i)}$表示”输出”变量(“output” variables)，也称为目标值(target)。
一对$(x^{(i)},y^{(i)})$称为一个训练样本(training example)，用作训练的数据集就是就是一组$m$个训练样本${(x^{(i)},y^{(i)});i=1,…,m}$，被称为训练集(training set)。
$X$表示输入变量的取值空间，$Y$表示输出变量的取值空间。那么$h:X \rightarrow Y$是训练得到的映射函数，对于每个取值空间X的取值，都能给出取值空间Y上的一个预测值。函数$h$的含义为假设(hypothesis)。
图形化表示整个过程：

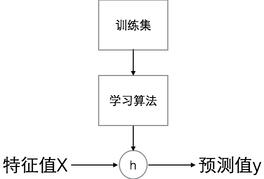
当预测值y为连续值时，则有监督学习问题是回归(regression)问题；预测值y为离散值时，则为分类(classification)问题。

线性回归(Linear Regression)

先简单将y表示为x的线性函数：

$$h(x) = \sum_{i=0}^{n}\theta _ix_i=\theta^Tx$$

$\theta$ 称为参数(parameters)，也叫做权重(weights)，参数决定了$X$到$Y$的射映空间。
用$x_0=1$来表示截距项(intercept term)。

有了训练集，如果通过学习得到参数$\theta$？

一种方法是，让预测值$h(x)$尽量接近真实值y，定义成本函数(cost function):

$$J(\theta) = \frac12\sum_{i=1}^{m}(h_{\theta}(x_i)-y_i)^2$$

这实际上就是最小二乘成本函数，我们把这个回归模型叫做普通最小二乘回归模型(ordinary least squares regression model)。

LMS算法

为了找到使成本函数$J(\theta)$最小的参数$\theta$，采用搜索算法：给定一个$\theta$的初值，然后不断改进，每次改进都使$J(\theta)$更小，直到最小化$J(\theta)$的$\theta$的值收敛。

考虑梯度下降(gradient descent)算法：从初始$\theta$开始，不断更新：

$$\theta_j:=\theta_j-\alpha \frac{\delta}{\delta\theta_j}J(\theta)$$

注意，更新是同时对所有$j=0,…,n$的$\theta_j$值进行。$\alpha$被称作学习率(learning rate)，也是梯度下降的长度，若$\alpha$取值较小，则收敛的时间较长；相反，若$\alpha$取值较大，则可能错过最优值。

假设我们只有一个训练样本$(x,y)$，此时$J(\theta) = \frac12(h_{\theta}(x)-y)^2$，求偏导项得到：

$$\begin{equation} \begin{split} \frac{\delta}{\delta\theta_j}J(\theta) =& \frac{\delta}{\delta\theta_j}\frac12(h_{\theta}(x)-y)^2\\ =& (h_{\theta}(x)-y)*\frac{\delta}{\delta\theta_j}(h_{\theta}(x)-y)\\ =& ((h_{\theta}(x)-y))*\frac{\delta}{\delta\theta_j}(\sum_{i=0}^{n}\theta_ix_i-y)\\ =& (h_{\theta}(x)-y)*x_j \end{split} \end{equation}$$

每次按照以下式子更新$\theta_j$的值：

$$\theta_j:=\theta_j+\alpha(y^{(i)}-h_{\theta}(x^{(i)}))*x_j^{(i)}$$

这种更新方法叫做LMS更新策略(Least Mean Squares update rule)，也叫做Widrow-Hoff 学习策略。

采用LMS方法，参数更新的次数和误差项$(y^{(i)}-h_{\theta}(x^{(i)}))$成正比。也就是说，如果预测值与真实值的误差项较小，则参数调整改变不会很大，相反，如果误差项较大，参数进行的调整更大。

如果训练集不只一个训练样本，可以采用以下方法更新参数：

Repeat until convergence{

$\theta_j:=\theta_j+\alpha\sum_{i=1}^m(y^{(i)}-h_\theta(x^{(i)})x_j^{(i)})$ (for every j)

}

实际上，这里的求和刚好是$\frac{\delta J(\theta)}{\delta\theta_j}$的值。这种方法每一步更新都会遍历每所有的训练样本，因此被称作批量梯度下降(batch gradient descent)。

梯度下降法通常容易受局部最优值的影响，但这里的最优问题只有一个全局最优值，没有局部最优值。因此梯度下降总是收敛到全局最优解（学习率$\alpha$不能取太大，否则错过最优值）。

除了批量梯度下降，还有一种方法叫做随机梯度下降(stochastic gradient descent)，也叫做增量梯度下降(incremental gradient descent)。其更新策略为：

Loop{

for i=1 to m,{

$\theta_j:=\theta_j+\alpha(y^{(i)}-h_{\theta}(x^{(i)}))x_j^{(i)}$ (for every j).

}

随机梯度下降和批量梯度下降不同点在于，批量梯度下降每一步更新$\theta$值，都需要遍历全部的训练样本，而随机梯度下降在遇到每个训练样本时，更新$\theta$之后继续处理下一个样本，每个样本只遍历一次，算法的学习时间比批量梯度下降快很多。但是，随机梯度下降可能永远不会收敛到全局最优值，而是在成本函数$J(\theta)$最优值周围附近摇摆。但是在实际问题中，接近最优值的参数值可能已经是足够好的结果了，特别是对于数据量非常大的训练集来说，随机梯度下降是比批量梯度下降更好的选择。

在实际使用梯度下降算法时，将输入变量归一到同一取值范围，能够减少算法的迭代次数。这是因为$\theta$在小的取值范围内会下降很快，但在大的取值范围内会下降较慢。并且当输入变量取值范围不够均衡时，$\theta$更容易在最优值周围波动。采用特征缩放(feature scaling)和均值归一化(mean normalization)可以避免这些问题。选择学习率$\alpha$的值，要观察$J(\theta)$值在每次迭代后的变化。已经证明了如果$\alpha$的取值足够小，则$J(\theta)$每次迭代后的值都会减少。如果$J(\theta)$在某次迭代后反而增加了，说明学习率$\alpha$的值应该减小，因为错过了最优值。Andrew Ng推荐的一个经验是每次将$\alpha$减少3倍。

正规方程(The normal equations)

梯度下降是最小化$J(\theta)$的一种方式，正规方程是另一种求解参数$\theta$的方法，这种方法可以直接求出最优值参数结果，不需要迭代更新，也不需要事先对数据进行归一化预处理。这种方法实际上是直接求出$J(\theta)$的导数，并令其为0。

$$J(\theta)=\sum_{i=1}^m(h_{\theta}(x^{(i)}-y^{(i)}))^2=\frac12(X\theta-\overrightarrow y)^T(X\theta-\overrightarrow y)$$ $$\nabla_{\theta}J(\theta)=0$$

解之，

$$\nabla_{\theta}J(\theta) = X^TX\theta-X^T\overrightarrow y=0$$

得到正规方程：

$$X^TX\theta=X^T\overrightarrow y$$

求解$\theta$：

$$\theta=(X^TX)^{-1}X^T\overrightarrow y$$

正规方程求解$\theta$的时间复杂度为$O(n^3)$，n是特征数量。当特征数量很大时，正规方程求解会很慢。Andrew Ng给出的一个经验参考是：当n>10,000时，采用梯度下降比正规方程更好。

比较一下正规方程和梯度下降：

正规方程	梯度下降
不需要调整参数	需要调整参数$\alpha$
不需要迭代	需要迭代更新$\theta$值
n较大时效率低	n较大时效率也不错

正规方程还会遇到$X^TX$不可逆的情况，通常这是因为输入变量中存在线性相关的变量或者是因为特征太多($n\geq m$)。解决方法是去掉线性相关的冗余变量，或者删掉一些特征。

机器学习笔记1 有监督学习 线性回归 LMS算法 正规方程

有监督学习

线性回归(Linear Regression)

LMS算法

正规方程(The normal equations)

机器学习笔记1 有监督学习线性回归 LMS算法正规方程